Here are the problems and rules of the contest in English and in Russian.

Minor changes:

Problem 1. 123456789   $\longrightarrow$  12345678987654321

Problem 10. An 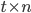$t\times n$ matrix 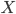$X$, where 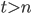$t>n$, in which each element is zero or one is such that each column contains exactly $s+1$ ones... 

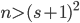
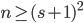Problem 10. $n> (s+1)^2$   $\longrightarrow$   $n\geq (s+1)^2$.

Rules.

1. The olympiad is mainly aimed at undergraduate students, but it is also open to other participants (including high-school students).
2. We recommend sending solutions in PDF format. Please write your name, email, university and year of university education (if you are a student) on the first page of the document with solutions. The solutions can be sent to comb.olymp@phystech.edu before 15.05.2019.
3. The full solution of each problem will be graded by 10 points, the partial solutions will be also graded.
4. If you have any questions, please email us at comb.olymp@phystech.edu.
5. The results will be available here: https://polyanskii.com/other/combolymp/

The olympiad is organized by the Department of Discrete Mathematics of Moscow Institute of Physics and Technology (State University). Here is information about our international master’s programs and other opportunities:

• Advanced Combinatorics: https://advcombi.org/
• Contemporary Combinatorics: https://comb-mipt.ru/
• Computer Science: https://cs-mipt.ru/
• Deep Learning School: https://www.dlschool.org/?lang=en

If you have any questions about programs, please email Prof. Andrei Michailovich Raigorodskii at mraigor@yandex.ru.